Fundamental Wave Properties

View Assign Share Link Report

Fundamental Wave Properties

This lesson aligns with NGSS PS4.A

Introduction

A wave can be defined as a disturbance that travels through a medium, transferring energy from one point to another without causing a permanent displacement of the medium itself. From light waves enabling us to see, to sound waves that allow us to hear, waves play a crucial role in various natural phenomena and technological applications. In this article, we will explore these core properties and how they are mathematically described and applied.

Types of Wave

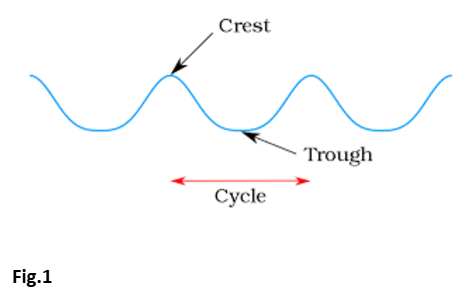
Waves are generally classified into two types:

Mechanical Waves: These waves require a medium to propagate, such as water waves, sound waves in air, and seismic waves.
Electromagnetic Waves: These waves can travel through a vacuum without a medium, including light, radio waves, and X-rays.

Regardless of the type, all waves share the properties of amplitude, wavelength, and frequency.

Amplitude:

The amplitude of a wave refers to the maximum displacement of the wave from its equilibrium position. It represents the height of the wave crest (or depth of the trough), and is a direct measure of the energy carried by the wave. Mathematically, amplitude is often denoted as A.

In the case of mechanical waves like sound, amplitude correlates with intensity. For example, a louder sound has a higher amplitude, while a softer sound has a lower amplitude.

For mechanical waves, amplitude can be represented as:

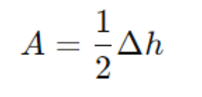
Where:

A is the amplitude
Δh is the total height of the wave from crest to trough

For electromagnetic waves, amplitude affects the electric and magnetic field strengths. Although it doesn't determine the frequency or speed, it is an essential component of the wave's overall energy.

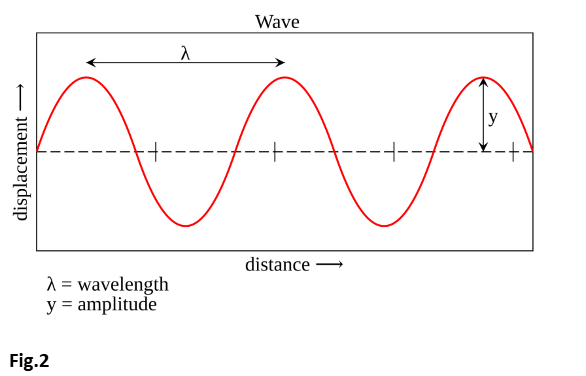
Wavelength: The Distance Between Wave Crests

The wavelength of a wave is the distance between two successive points in phase, such as the distance from one crest to the next or one trough to the next. Wavelength is denoted by the Greek letter λ(lambda), and it is typically measured in meters, although the unit can vary depending on the type of wave.

The formula for wavelength is:

λ=v/f

For example, in electromagnetic waves, wavelength determines the type of radiation. Shorter wavelengths correspond to higher-energy waves, such as ultraviolet light and X-rays, while longer wavelengths correspond to lower-energy waves, like infrared radiation and radio waves.

Frequency: The Number of Oscillations Per Second

Frequency refers to the number of complete wave cycles (oscillations) that pass a given point per second. It is measured in Hertz (Hz), where 1 Hz equals one cycle per second. Frequency is denoted as f, and it is inversely related to wavelength.

The relationship between frequency and wavelength is given by the formula:

f=vλ

Frequency plays a critical role in determining the nature of a wave. For example, in sound waves, frequency determines the pitch of the sound. High-frequency waves produce high-pitched sounds, such as the sound of a whistle, while low-frequency waves produce low-pitched sounds, like the rumble of thunder.

In electromagnetic waves, frequency determines the type of wave within the electromagnetic spectrum. For instance, visible light ranges from about 430 terahertz (THz) for red light to about 770 THz for violet light. Radio waves, on the other hand, operate at much lower frequencies, while X-rays and gamma rays have very high frequencies.

The Wave Speed Equation

The speed at which a wave travels through a medium is called wave speed and is denoted by v. Wave speed depends on the medium through which the wave is propagating and the type of wave in question. For example, sound waves travel faster in water than in air, and electromagnetic waves travel fastest in a vacuum.

The wave speed equation, which relates wave speed to wavelength and frequency, is given by:

v=λf

Where:

v is the wave speedλ is the wavelength
f is the frequency

This formula shows that wave speed is the product of wavelength and frequency. If the speed of the wave remains constant, an increase in frequency will result in a decrease in wavelength, and vice versa.

Relationships Between Amplitude, Wavelength, and Frequency

Amplitude, wavelength, and frequency are related in various ways, depending on the type of wave. However, they are independent properties. For instance, changing the amplitude of a wave affects the wave’s energy but does not affect its wavelength or frequency. Similarly, altering the frequency of a wave changes the wavelength, but the amplitude remains unaffected.

For electromagnetic waves, the energy of the wave is related to its frequency and amplitude. Higher frequency waves carry more energy, as expressed by the formula for the energy of a photon:

E=hf

Where:

E is the energy of the photon
h is Planck's constant
f is the frequency of the wave

Conclusion

A wave is a disturbance that travels through a medium, transferring energy from one point to another without causing a permanent displacement of the medium itself.
The amplitude of a wave refers to the maximum displacement of the wave from its equilibrium position.
The wavelength of a wave is the distance between two successive points in phase, such as the distance from one crest to the next or one trough to the next.
Frequency refers to the number of complete wave cycles (oscillations) that pass a given point per second. It is measured in Hertz (Hz).

Related Worksheets: