Energy Conservation in Torsional Systems

View Assign Share Link Report

Energy Conservation in Torsional Systems

This lesson aligns with NGSS PS3.B

Introduction

In torsional systems—such as twisting rods, shafts, or torsion springs—energy conservation principles apply similarly to linear mechanical systems, although the energy is stored and transformed in rotational, rather than translational, motion. This article will explore the concept of energy conservation in torsional systems, examine the potential energy stored in twisted objects, and delve into the kinetic energy during oscillations.

Torsional Systems and Energy Conservation

In torsional systems, energy can exist in different forms, primarily as potential energy and kinetic energy. These systems involve rotational motion, which can be caused by the twisting of rods or the deformation of torsion springs.

The conservation of energy in torsional systems follows the same principle as in linear systems: the total mechanical energy remains constant in the absence of non-conservative forces, such as friction or air resistance. The mechanical energy is conserved as it oscillates between potential energy (stored in the twisted object) and kinetic energy.

Potential Energy in Twisted Objects

When an object, such as a rod or torsion spring, is twisted, potential energy is stored within the material due to its deformation. This energy is called torsional potential energy and depends on the object's material properties, geometry, and the amount of twist applied. For a linear elastic material, the potential energy stored in the twisted object is proportional to the square of the angular displacement.

For torsion springs or rods, the potential energy can be mathematically described using the equation:

Where:

U is the potential energy stored in the system,
$k_theta$ is the torsional stiffness (or torsional spring constant),
θ is the angular displacement from the equilibrium position.

The torsional stiffness

$k_theta$ represents the resistance of the material to twisting and depends on both the material properties and the geometric configuration of the system. In the case of cylindrical rods, for instance, the stiffness is influenced by factors such as the material's shear modulus and the rod's length and radius.

Example: Torsion Spring

Torsion springs are a common example of torsional systems where energy is stored in the form of torsional potential energy. These springs work by twisting rather than compressing or stretching, as seen in traditional linear springs. When the spring is twisted, the material stores energy proportional to the square of the angular displacement, following the formula mentioned earlier.

Consider a torsion spring in a mousetrap. When the trap is set, the spring is twisted by a certain angle

$theta$ . As the spring is twisted, potential energy is stored in it. When the trap is triggered, the stored potential energy is released and converted into kinetic energy, allowing the trap to snap shut.

Kinetic Energy in Torsional Systems

In addition to potential energy, torsional systems also exhibit kinetic energy during rotational motion. When an object that has been twisted is released, the stored potential energy is transformed into kinetic energy as the object rotates. The rotational kinetic energy is associated with the object's angular velocity and can be expressed as:

Where:

KE is the kinetic energy,
I is the moment of inertia of the object,
$omega$ is the angular velocity.

The moment of inertia I is a measure of how the object's mass is distributed with respect to the axis of rotation. It plays a similar role in rotational dynamics as mass does in linear dynamics. The greater the moment of inertia, the more resistance the object has to changes in its rotational motion.

Example: Twisting a Rod

Imagine a metal rod that is twisted at one end while the other end is fixed. As the rod is twisted, potential energy is stored within it due to the deformation of its material. When the rod is released, this stored potential energy is converted into rotational kinetic energy, causing the rod to oscillate back and forth.

The energy conservation principle ensures that, in the absence of energy losses due to friction or air resistance, the total mechanical energy of the system remains constant. The potential energy stored at the peak of the twist will convert to kinetic energy as the rod untwists and oscillates. At the equilibrium position (where the rod is not twisted), all the energy will be in the form of kinetic energy. As the rod continues to oscillate, the energy will continuously shift between potential and kinetic forms.

Energy Oscillations in Torsional Systems

In ideal torsional systems, where no energy is lost to friction or other non-conservative forces, the system exhibits harmonic oscillations. These oscillations are governed by the interplay between potential energy and kinetic energy. When the torsion spring or rod reaches its maximum angular displacement, all of the energy is stored as potential energy. As the object moves toward the equilibrium position, the potential energy is converted into kinetic energy.

The motion in such a system can be compared to simple harmonic motion in linear systems, where energy oscillates between kinetic and potential forms. The angular frequency of the oscillation in a torsional system is given by:

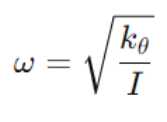
Where

$omega$ is the angular frequency of the system,

$k_theta$ is the torsional stiffness, and I is the moment of inertia. This equation shows that the frequency of the oscillation depends on both the torsional stiffness of the material and the moment of inertia of the object.

Conclusion

When an object, such as a rod or torsion spring, is twisted, potential energy is stored within the material due to its deformation. This energy is called torsional potential energy.
It depends on the object's material properties, geometry, and the amount of twist applied.
For a linear elastic material, the potential energy stored in the twisted object is proportional to the square of the angular displacement.

Related Worksheets: