Damped Oscillations and Energy Loss

View Assign Share Link Report

Damped Oscillations and Energy Loss

This lesson aligns with NGSS PS3.B

Introduction

Oscillatory motion is a fundamental concept where an object repeatedly moves back and forth around an equilibrium position. Classic examples include a mass-spring system or a pendulum. In ideal conditions, such oscillations are undamped, meaning they continue indefinitely without losing energy. However, in practical scenarios, damping effects such as friction, air resistance, or internal material resistance play a crucial role, causing energy loss over time. This article explores how energy conservation is impacted in systems with damping, focusing on the behavior of damped oscillations and the mechanisms of energy loss.

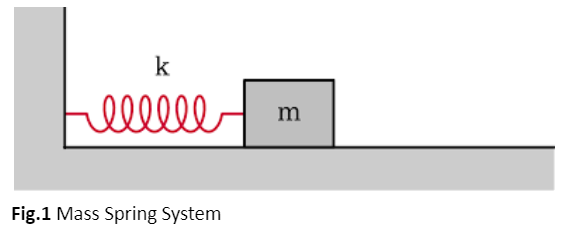
The Ideal Oscillatory System

In an ideal mass-spring system, the motion of the mass attached to the spring is governed by Hooke's Law, which states that the force exerted by the spring is proportional to its displacement from the equilibrium position:

F=−kx

1. Kinetic Energy (KE):

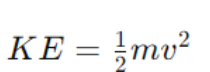
where m is the mass of the object and v is its velocity.

2. Potential Energy (PE):

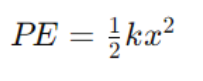
At any point in the oscillation, the total mechanical energy E is the sum of kinetic and potential energy:

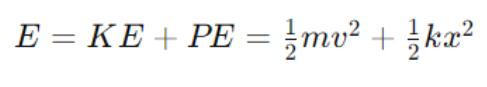
In an ideal system with no damping, this total mechanical energy remains constant, as the energy is merely converted between kinetic and potential forms.

Introduction to Damping

Oscillatory systems experience damping due to various factors such as friction, air resistance, or internal material hysteresis. Damping introduces a resistive force that is typically proportional to the velocity of the object:

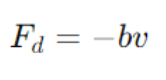
where b is the damping coefficient and v is the velocity. This non-conservative force leads to a gradual loss of mechanical energy, altering the system's behavior.

Mathematical Description of Damped Oscillations

The introduction of damping changes the equation of motion for a mass-spring system from:

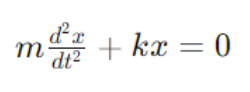
To:

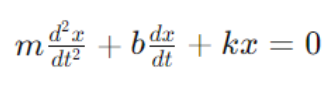
This is a second-order linear differential equation where the term b

$dx/dt$ represents the damping force.

The solution to this differential equation depends on the damping condition:

1. Underdamping:

Occurs when the damping force is relatively small. The system oscillates with an amplitude that decreases exponentially over time. The general solution is:

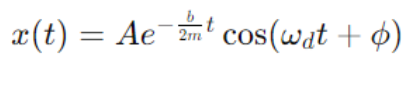
where A is the initial amplitude,

$phi$ is the phase constant, and

$omega_d$ is the damped angular frequency:

2. Critical Damping:

This occurs when the damping is just enough to prevent oscillation. The system returns to equilibrium as quickly as possible without oscillating. The solution is:

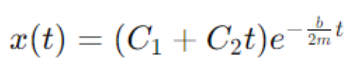
3.Overdamping:

When damping is excessive, the system returns to equilibrium slowly without oscillating. The solution is:

where

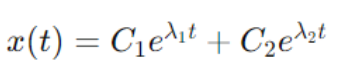
$lambda_1$ and

$lambda_2$ are the roots of the characteristic equation associated with the differential equation.

Energy Loss in Damped Systems

In a damped system, energy is not conserved. Instead, mechanical energy is continually lost due to the work done against the damping force. The total mechanical energy E(t) at time t is the sum of the kinetic and potential energies:

where:

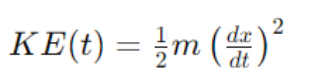
And

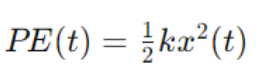
The rate at which mechanical energy is lost due to damping can be calculated by examining the power dissipated by the damping force:

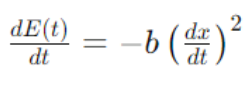
This shows that the power dissipated is proportional to the square of the velocity. Integrating this over time provides the total energy lost:

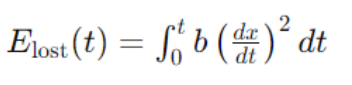
Predicting System Behavior

The presence of damping affects the behavior of the oscillatory system. For underdamped systems, the amplitude of oscillation decreases exponentially over time. The amplitude A(t) at time t can be expressed as:

where

$A_0$ is the initial amplitude. The time constant

$tau$ is:

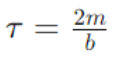
which characterizes the rate at which the amplitude decreases.For critically damped and overdamped systems, the system does not oscillate but instead returns to equilibrium at a rate dependent on the damping coefficient and system parameters. The behavior can be predicted by solving the differential equations specific to critical and overdamped cases.

Conclusion

Oscillatory motion is a fundamental concept where an object repeatedly moves back and forth around an equilibrium position.
Classic examples include a mass-spring system or a pendulum.
Oscillatory systems experience damping due to various factors such as friction, air resistance, or internal material hysteresis.
Damping introduces a resistive force that is typically proportional to the velocity of the object.
In a damped system, energy is not conserved. Instead, mechanical energy is continually lost due to the work done against the damping force.

Related Worksheets: