Elastic and Inelastic Collisions

View Assign Share Link Report

Elastic and Inelastic Collisions

This lesson aligns with NGSS PS3.B

Introduction

A collision occurs when two or more bodies exert forces on each other for a short period of time. The result of the collision depends on the forces involved, the mass of the objects, and the type of collision. Among the most critical types of collisions are elastic and inelastic collisions, which are defined by the behavior of kinetic energy before and after impact. This article will compare and contrast elastic and inelastic collisions, focusing on the conservation of energy and the prediction of post-collision velocities using mathematical principles.

Collisions

In both elastic and inelastic collisions, momentum is conserved. The total momentum of the system before the collision is equal to the total momentum of the system after the collision. Mathematically, momentum conservation is expressed as:

where:

$m_1$ and $m_2$ are the masses of the two colliding objects,
$v_1$ and $v_2$ are their velocities before the collision,
$v'_1$ and $v'_2$ are their velocities after the collision.

Elastic Collisions

In an elastic collision, both momentum and kinetic energy are conserved. The total kinetic energy of the system remains the same before and after the collision. This type of collision typically occurs in idealized systems where external forces like friction and air resistance are negligible.

Elastic collisions often involve objects that do not experience deformation upon impact, such as atoms or subatomic particles. However, in everyday life, elastic collisions are approximations seen in scenarios like two billiard balls striking each other or two rubber balls bouncing off one another.

Conservation of Kinetic Energy

For an elastic collision, the total kinetic energy before and after the collision is the same. The equation representing the conservation of kinetic energy is:

This means that no kinetic energy is lost as heat, sound, or deformation during the collision. The velocities of the objects may change, but the total kinetic energy remains constant.

Solving Elastic Collisions

To predict the final velocities in a one-dimensional elastic collision, we can solve two simultaneous equations: one for the conservation of momentum and another for the conservation of kinetic energy.

For simplicity, assume two objects with masses

$m_1$ and

$m_2$ , and initial velocities

$v_1$ and

$v_2$ . After the collision, their final velocities are

$v'_1$ and

$v'_2$ .

The equations are:

1.Momentum conservation:

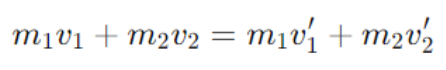
2. Kinetic energy conservation:

Using algebra, we can derive the final velocities for a one-dimensional elastic collision:

These formulas enable us to predict the post-collision velocities of the two objects. The key takeaway in elastic collisions is that the objects retain their total kinetic energy, even though individual objects may gain or lose kinetic energy.

Inelastic Collisions

In contrast, an inelastic collision does not conserve kinetic energy. While momentum is still conserved, some of the kinetic energy is transformed into other forms of energy, such as heat, sound, or internal energy, leading to deformation of the colliding objects.

A perfectly inelastic collision represents the extreme case, where the colliding objects stick together after impact and move with a common velocity.

Loss of Kinetic Energy

In an inelastic collision, the total kinetic energy of the system after the collision is less than the total kinetic energy before the collision. This energy loss is due to the conversion of kinetic energy into other forms of energy. The equation for the total kinetic energy after the collision becomes:

Unlike elastic collisions, where energy is transferred between objects but the total remains the same, inelastic collisions result in a net loss of kinetic energy.

Solving Inelastic Collisions

In the case of a perfectly inelastic collision, the two objects stick together and move as one mass after the collision. The conservation of momentum equation is sufficient to determine the final velocity of the combined mass. Let

$v_f$ represent the final velocity of the combined objects. Momentum conservation gives:

Solving for

$v_f$ :

This equation allows us to determine the final velocity after the collision, but kinetic energy is not conserved. The amount of kinetic energy lost can be calculated by comparing the total kinetic energy before and after the collision:

This energy difference represents the energy lost to heat, deformation, and other non-kinetic forms.

Comparing Elastic and Inelastic Collisions

Elastic collisions: Momentum and kinetic energy are both conserved. Examples include collisions between hard spheres like billiard balls or atoms in idealized conditions.

Inelastic collisions: Only momentum is conserved, while some kinetic energy is lost to deformation, heat, or other energy forms. Perfectly inelastic collisions, where objects stick together, represent the extreme case.

In real-world scenarios, most collisions fall somewhere between perfectly elastic and perfectly inelastic.

For instance, car accidents typically involve significant deformation, resulting in inelastic collisions. On the other hand, molecular collisions, particularly in gases, are often approximated as elastic.

Conclusion

A collision occurs when two or more bodies exert forces on each other for a short period of time.
The result of the collision depends on the forces involved, the mass of the objects, and the type of collision.
In an elastic collision, both momentum and kinetic energy are conserved. The total kinetic energy of the system remains the same before and after the collision.
In contrast, an inelastic collision does not conserve kinetic energy.

Related Worksheets: