Spring Systems and Hooke's Law

View Assign Share Link Report

Spring Systems and Hooke's Law

This lesson aligns with NGSS PS3.B

Introduction

A spring system typically consists of an elastic object (the spring) that can be compressed or stretched. Springs are designed to store and release mechanical energy. One of the fundamental concepts in this realm is Hooke's Law, which describes how springs respond to forces. This article explores spring systems, Hooke's Law, and provides mathematical expressions and practical examples to illustrate these principles.

Understanding Spring Systems

When a force is applied to a spring, it deforms, and upon removing the force, the spring returns to its original shape. This property makes springs ideal for applications requiring energy absorption, storage, and release.

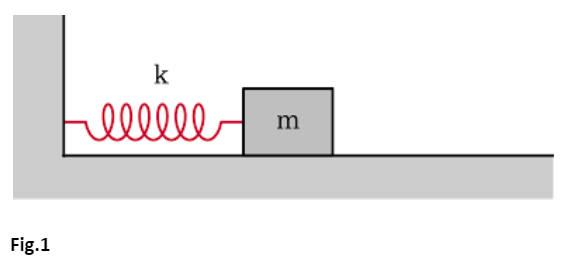
Hooke's Law

Hooke's Law is a principle of physics that states that the force needed to extend or compress a spring by some distance is proportional to that distance. Mathematically, Hooke's Law is expressed as:

Where:

F is the force exerted by the spring (in newtons, N).
k is the spring constant (in newtons per meter, N/m), a measure of the spring's stiffness.
x is the displacement of the spring from its equilibrium position (in meters, m).
The negative sign indicates that the force exerted by the spring is in the opposite direction of the displacement.

Spring Constant (k)

The spring constant k is a crucial parameter in Hooke's Law. It quantifies the stiffness of a spring; a higher k value indicates a stiffer spring that requires more force to achieve the same displacement. The spring constant depends on the material and geometry of the spring.

Types of Springs

There are several types of springs, each serving different purposes:

Compression Springs:

Designed to operate with a compression load, meaning they get shorter when a force is applied.

Extension Springs:

Work with a tension load; they extend when a force is applied.

Torsion Springs:

Function by twisting; the force applied causes the spring to twist rather than compress or extend.

Potential Energy in Springs

When a spring is displaced from its equilibrium position, it stores potential energy. The potential energy U stored in a spring is given by:

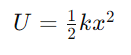
This equation shows that the potential energy is proportional to the square of the displacement, meaning that as the spring is stretched or compressed further, the stored energy increases quadratically.

Examples of Hooke's Law

Example 1: Compression Spring

Consider a compression spring with a spring constant k=200 N/m. If the spring is compressed by 0.1 m, the force exerted by the spring can be calculated using Hooke's Law:

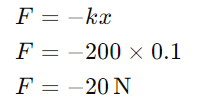
The negative sign indicates that the force is in the opposite direction of the displacement, i.e., the spring is pushing back against the compression.

Example 2: Extension Spring

For an extension spring with k=150N/m, if the spring is stretched by 0.2 m, the force exerted by the spring is:

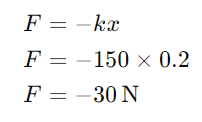
Again, the negative sign shows that the force exerted by the spring opposes the stretching.

Oscillations in Spring Systems

When a spring is displaced and released, it often undergoes oscillatory motion. This motion can be analyzed using Hooke's Law and principles of simple harmonic motion (SHM).

Simple Harmonic Motion

In SHM, the restoring force is directly proportional to the displacement and acts in the opposite direction. For a mass m attached to a spring with spring constant k, the equation of motion is:

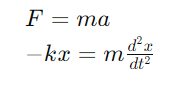
This can be rewritten as:

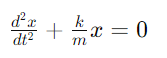
The general solution to this differential equation is:

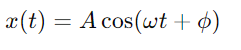
Where:

A is the amplitude of the oscillation.
$omega$ is the angular frequency.
$phi$ is the phase constant, determined by the initial conditions.

Period and Frequency

The period T of oscillation is the time it takes for one complete cycle and is given by:

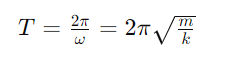
The frequency f, the number of oscillations per unit time, is:

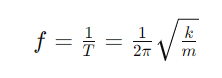
Conclusion

A spring system typically consists of an elastic object (the spring) that can be compressed or stretched.
Hooke's Law states that the force needed to extend or compress a spring by some distance is proportional to that distance.
When a spring is displaced from its equilibrium position, it stores potential energy.
Potential energy is proportional to the square of the displacement, meaning that as the spring is stretched or compressed further, the stored energy increases quadratically.

Related Worksheets: