Spin and Magnetic Moments

View Assign Share Link Report

Spin and Magnetic Moments

This lesson aligns with NGSS PS2.B

Introduction

The concepts of spin and magnetic moments are fundamental to the fields of quantum mechanics, condensed matter physics, and electromagnetism. These properties are crucial for understanding the behavior of subatomic particles, atoms, and materials in magnetic fields. This article delves into the nature of spin, its relationship with magnetic moments, and the implications for both theoretical physics and practical applications.

Understanding Spin

Spin is an intrinsic form of angular momentum carried by elementary particles, composite particles (hadrons), and atomic nuclei. Unlike classical angular momentum, which arises from a particle’s motion through space, spin is a quantum mechanical property that does not have a direct classical analogue.

Quantum Nature of Spin

In quantum mechanics, spin is characterized by a quantum number, denoted as s, which can take on half-integer or integer values. For example, electrons, protons, and neutrons have a spin of 1/2, while photons have a spin of 1. The value of the spin quantum number determines the possible orientations of the spin angular momentum along a given axis.

The z-component of the spin angular momentum

$S_Z$ is quantized and given by:

Where

$m_s$ is the spin magnetic quantum number, which can take on values from −s to +s in integer steps, and ℏ is the reduced Planck constant.

Spin and Magnetic Moments

The magnetic moment associated with a particle’s spin is a critical aspect of its interaction with magnetic fields. The spin magnetic moment μS is proportional to the spin angular momentum S:

Here,

$g_s$ is the g-factor specific to the particle (approximately 2 for electrons), e is the elementary charge, and m is the mass of the particle. The negative sign indicates that the magnetic moment and the spin angular momentum are antiparallel for electrons.

Electron Spin and Magnetic Moments

Electrons possess both orbital and spin magnetic moments. The total magnetic moment μ of an electron in an atom is the vector sum of its orbital

$mu_L$ and spin

$mu_S$ magnetic moments:

For an electron moving in an atomic orbital, the orbital magnetic moment

$mu_L$ is given by:

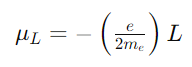
Where

L is the orbital angular momentum vector. The total magnetic moment thus reflects both the electron’s motion around the nucleus and its intrinsic spin.

Pauli Exclusion Principle and Spin
The Pauli Exclusion Principle, a fundamental principle in quantum mechanics, states that no two fermions (particles with half-integer spin) can occupy the same quantum state simultaneously. This principle is crucial in determining the electronic structure of atoms and the properties of materials. Electrons, being fermions, must have unique sets of quantum numbers, including their spin states, within an atom.

Spin-Orbit Coupling

Spin-orbit coupling is a phenomenon where an electron’s spin interacts with its orbital motion around the nucleus. This interaction leads to energy level splitting, known as fine structure, in atomic spectra. Spin-orbit coupling is responsible for various important effects in solid-state physics, such as the splitting of electronic bands in crystals and the formation of topologically protected states in materials with strong spin-orbit interactions.

Experimental Techniques for Studying Spin and Magnetic Moments

Several experimental techniques are used to investigate spin and magnetic moments:

Electron Spin Resonance (ESR):
Also known as electron paramagnetic resonance (EPR), this technique detects the transitions between spin states of unpaired electrons in a magnetic field, providing information about the electronic structure and environment of paramagnetic species.
Mössbauer Spectroscopy:
This technique studies the resonant absorption of gamma rays by nuclei, providing detailed information about the nuclear magnetic moments and the local magnetic environment.
Magnetic Force Microscopy (MFM):
MFM is a type of scanning probe microscopy that maps the magnetic structure of surfaces with high spatial resolution, revealing information about the distribution of magnetic moments in materials.
Neutron Scattering:
Neutrons, having a magnetic moment, interact with the magnetic moments in materials. Neutron scattering experiments provide detailed information about the magnetic order and excitations in materials.

Conclusion

Spin is an intrinsic form of angular momentum carried by elementary particles, composite particles (hadrons), and atomic nuclei.
Spin is a quantum mechanical property that does not have a direct classical analogue.
The magnetic moment associated with a particle’s spin is a critical aspect of its interaction with magnetic fields. The spin magnetic moment μS is proportional to the spin angular momentum S.
Spin-orbit coupling is a phenomenon where an electron’s spin interacts with its orbital motion around the nucleus.
This interaction leads to energy level splitting, known as fine structure, in atomic spectra.

Related Worksheets: