Gauss's Law for Electricity

View Assign Share Link Report

Gauss's Law for Electricity

This lesson aligns with NGSS PS2.B

Introduction Gauss's law for electricity, one of Maxwell's equations, is a cornerstone of classical electromagnetism. This law provides a profound connection between electric charges and the electric field they generate. By exploring its mathematical formulation, physical interpretation, and practical applications, we can gain a comprehensive understanding of this fundamental principle.

Mathematical Formulation of Gauss's Law for Electricity Gauss's law for electricity states that the total electric flux through a closed surface is directly proportional to the total electric charge enclosed within that surface. Mathematically, it is expressed as:

where:

E is the electric field,
dA is a vector representing an infinitesimal area on the closed surface
S, oriented perpendicular to the surface,
$Q(enc)$ is the total electric charge enclosed within the surface
$ϵ_0$ is the permittivity of free space.

In differential form, Gauss's law for electricity can be written as:

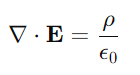
Where ∇⋅E represents the divergence of the electric field, and ρ is the charge density.

Physical Interpretation of Gauss's Law for Electricity Gauss's law provides a powerful tool for understanding how electric fields are generated by charge distributions. It essentially states that the electric flux through any closed surface is a measure of the net charge enclosed within that surface. This relationship implies several important concepts:

Electric Field Lines: Electric field lines originate from positive charges and terminate at negative charges. The number of field lines passing through a surface is proportional to the net charge enclosed.
Symmetry and Simplification: For symmetrical charge distributions, Gauss's law simplifies the calculation of electric fields. This is because the law allows us to relate the electric field to the charge enclosed by choosing an appropriate Gaussian surface.
Conservation of Flux: Gauss's law implies that electric flux is conserved. This means that the total flux entering a closed surface is equal to the total flux leaving it, reflecting the conservation of charge.

Gauss's law implies that electric flux is conserved. This means that the total flux entering a closed surface is equal to the total flux leaving it, reflecting the conservation of charge.

Practical Applications of Gauss's Law for Electricity

Electric Field of a Point Charge

One of the most straightforward applications of Gauss's law is to determine the electric field of a point charge Q. By considering a spherical Gaussian surface of radius r centered on the charge, we can derive Coulomb's law:

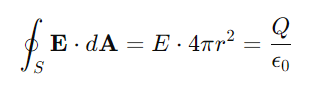
Solving for E, we obtain:

This shows that the electric field due to a point charge decreases with the square of the distance from the charge, and it points radially outward (or inward for a negative charge).

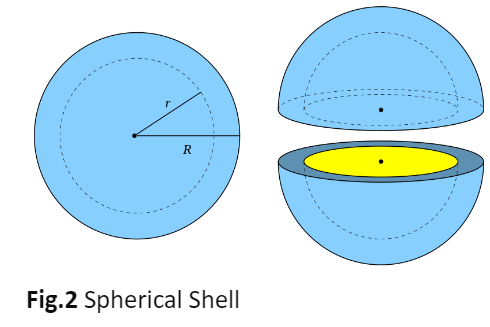
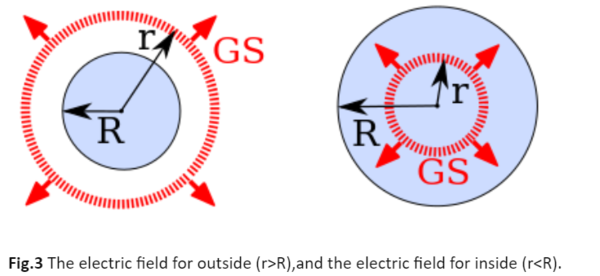
Electric Field of a Spherical Shell

Gauss's law is particularly useful for analyzing the electric field of a spherical shell with uniform charge distribution. Consider a spherical shell of radius R carrying a total charge Q:

Outside the Shell (r>R): The electric field behaves as if all the charge were concentrated at the center:

Inside the Shell (r<R): The electric field is zero, as no net charge is enclosed by a Gaussian surface within the shell:

E=0

Electric Field of an Infinite Plane For an infinite plane with a uniform surface charge density σ, we can use a cylindrical Gaussian surface with its axis perpendicular to the plane. The flux through the curved surface is zero due to the perpendicular electric field lines, leaving only the flux through the flat ends:

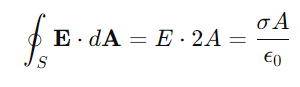
Solving for E, we get:

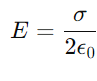
This result shows that the electric field due to an infinite plane of charge is constant and does not depend on the distance from the plane.

Electric Field of a Line of Charge For an infinite line of charge with linear charge density λ, we use a cylindrical Gaussian surface with its axis along the line of charge. The electric field is radial, and the flux through the curved surface is:

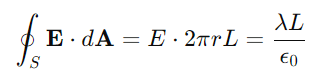
Solving for E, we obtain:

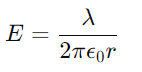
This indicates that the electric field due to an infinite line of charge decreases linearly with distance from the line.

Gauss's Law in Complex Charge Distributions Gauss's law is not limited to simple geometries. It can be applied to more complex charge distributions, often in conjunction with symmetry arguments to simplify the problem. By carefully choosing a Gaussian surface that takes advantage of the symmetry, the calculation of electric fields becomes more tractable.

Example: Electric Field of a Cylindrical Shell Consider a cylindrical shell of radius R and height L with a uniform surface charge density σ:

Outside the Shell: For a point outside the shell (r>R), a cylindrical Gaussian surface coaxial with the shell encloses all the charges. The electric field at distance r is given by:

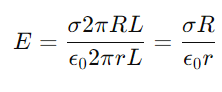
Inside the Shell: For a point inside the shell (r<R), the Gaussian surface encloses no charge, so the electric field is zero:

E=0

Example: Non-uniform Charge Distributions For non-uniform charge distributions, Gauss's law can still be applied, but the charge enclosed by the Gaussian surface must be integrated over the volume:

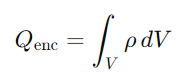
Where ρ is the charge density and dV is the volume element. This integral accounts for the varying charge density within the volume enclosed by the Gaussian surface.

Conclusion

Gauss's law for electricity states that the total electric flux through a closed surface is directly proportional to the total electric charge enclosed within that surface.
Electric field lines originate from positive charges and terminate at negative charges.
For symmetrical charge distributions, Gauss's law simplifies the calculation of electric fields.
Gauss's law implies that electric flux is conserved. This means that the total flux entering a closed surface is equal to the total flux leaving it, reflecting the conservation of charge.

Related Worksheets: